Предшественники
Софист Зенон Элейский (ок. 490 – ок. 430 до н.э.) знаменит своими парадоксами. Он составлял их для доказательства того, что бытие – едино, при этом не различая постоянное и преходящее. Для нас, однако, будет важна чисто математическая сторона его парадоксов, а не его метафизическая ошибка.
Когда Зенон говорит о том, что нельзя дойти до конца какого-либо пути, потому что сначала надо пройти полпути, затем половину оставшейся половины и т.д. до бесконечности, необходимо признать, что говорит он это не от того, что не может понять, что сумма ряда 1/2+1/4+1/8+ … равна 1. Напротив, говоря это, он указывает на саму немыслимость этого ряда как такового для человеческого сознания, именно этот ряд он и видит, и именно на его непомыслимость он и указывает.
Рене Декарт (1596 – 1650) – ключевая фигура в истории западноевропейской цивилизации в целом. Сейчас же нам будет важно лишь то, что введением “декартовых” координат в пространстве он “алгебраизировал” геометрию. Функция отождествилась со своим графиком (линия или поверхность), и таким образом геометрические задачи “без особых умственных усилий” (как особо настаивал сам Декарт) могут быть решены путём простых по своей структуре вычислений.
Простейший случай – пересечение двух кривых находится через решение системы из двух уравнений, а именно уравнений этих двух кривых. Не надо ничего чертить, не надо ничего “умопостигать”, надо только решить систему из двух уравнений и… перейти к следующей задаче.
Таким образом, открывалась довольно мрачная перспектива – перспектива изгнания из геометрии всякого творческого элемента. Всё то, за что ценили геометрию в древности, всё, что связано с неожиданными прозрениями, с полётом фантазии и пр. и пр., всему этому вдруг объявляется война, отныне творчество и фантазия должны быть раз и навсегда изгнаны. Не дóлжно “тратить умственные усилия” попусту, дóлжно лишь эффективно заниматься делом.
Так что, глядя на декартовы координаты, мы отчётливо начинаем слышать лязг индустриального железа.
И ещё одно маленькое отступление – насчёт того, что знание вроде бы и как бы должно быть непременно силой. Когда один из учеников Евклида спросил, что ему даст изучение геометрии в практическом отношении, Евклид обратился к своему рабу: “Дай ему три монеты, он хочет извлечь выгоду из учения”. Вот как жили во времена математической поэзии.
Готфрид Вильгельм Лейбниц (1646 – 1716) – великий математик, физик и философ. Ключевым в его философском и научном мировоззрении был принцип непрерывности. Всё в мире непрерывно, так что между двумя любыми явлениями любого рода мы, считал Лейбниц, всегда сможем найти промежуточное. Явившись одним из создателей исчисления бесконечно малых, Лейбниц видел в этом исчислении онтологию, сочетая учение о непрерывности с монадологией. Математический анализ у Лейбница становится зеркалом реальности в том, что касается бесконечности и непрерывности в окружающем нас мире.
Огюстен Луи Коши (1789 – 1857) – великий математик. Будучи искренним католиком, Коши категорически утверждает, что бесконечное есть единственно атрибут Бога, один Бог бесконечен, нигде, ни в мире, ни в мысли, актуально бесконечного нет и быть не может, и человек не вправе даже пытаться объять необъятное. Коши категорически выступает против любых инфинитезимальных построений в математике, против использования актуально бесконечно малых и бесконечно больших “величин”, против треугольников внутри точек, да и против рек внутри прозрачных плоскостей, о чём ниже. Сформулировав понятие предела, Коши радикально “рационализировал” математический анализ, сведя дело (точнее же, “как бы” сведя; век спустя выяснится, что полностью и в точном смысле такое на самом деле не представляется возможным) к рассмотрению потенциальной бесконечности.
Иоганн Дирихле (1805 – 1859) – великий математик. Нам важно будет то, что теорию функции Дирихле развивал опять-таки в сугубо “рациональном” ключе. Дирихле мыслил функцию только как “соответствие”, как класс упорядоченных пар. Никаких “чистых форм”, никаких “созерцаний” не допускается.

Наконец: Георг Кантор – главный enfant terrible и “гений и злодей” современной математики, математический Фауст и математический Мефистофель в одном лице. С его работами начинается “последний и решительный” метафизико-математический “штурм небес”. В его работах математика окончательно осознаёт себя как давно уже находящуюся в процессе этого “штурма” и решается на последний и отчаянный приступ в непосредственном предвидении столь, кажется, близкого “триумфа воли”.
Однако, такой вот “триумф воли” не состоялся и не состоится уже никогда. В частности же это означает, что Кантор не смог “решить” парадоксы Зенона.
Зенон оказался прав. До конца пути в аптеку мы дойдём, при необходимости даже и черепаху догоним, но произойдёт всё это совсем не так, как нам хотелось бы “думать”.
“Не геометр да не войдёт”
Каждый учёный любит свою науку. Историк любит историю, экономист – экономику, и математик математику.
При этом, например, историк любит историю не за возможность и даже необходимость дышать пылью в пыльных архивах. Историк полагает – и, конечно, не без оснований – что изучая историю, он, хотя бы отчасти, но всё же постигает судьбы мира.
Не за романтику составления бухгалтерской отчётности любит экономику экономист. Законы жизни, явленные в срезе хозяйственной деятельности – вот что интересует экономиста, вот что составляет для него подлинный интерес.
Иначе говоря, не сама наука, а как бы всегда нечто большее – вот за что учёные любят свою науку. Однако, как далеко это “большее” простирается, и насколько именно оно “больше”?
Вот поэтому всегда необходим некоторый критический взгляд, необходимо критически оценивать как полученные результаты, так и сами используемые методы. Ведь не познáет историк судьбы мира никогда и ни при каких условиях, и экономист никогда не сможет ответить на вопрос, что такое человек, хотя бы как “человек хозяйствующий”.
Но опаснее дело с математикой. Во-первых, просто шквал лести со всех сторон – как же, математика есть “царица наук”. Если историк без математики ещё кое-как справится, то экономист уже совсем никак, а о бедном физике и говорить нечего. Возникает ощущение всесилия, обладания философскими камнями и панацеями одновременно. Возникает ощущение нахождения в самом центре научно-познавательной деятельности, и потому иллюзия обладания “знанием как таковым”, “знанием самим по себе”. Математик – он уже как бы сам себе историк, сам себе экономист, физики вообще суть неудавшиеся математики, и что с ними говорить.
Во-вторых, завораживает точность и доказательность. Ведь рассматриваются и даже доказываются “вечные истины”, физические теории (а тем более экономические) появляются и исчезают как листья на ветру, но вот таблица умножения стоит как скала, возвышаясь и надмеваясь над суетой научного процесса.
Всё это создаёт почву для “математического шовинизма”, когда упоение точностью и вечностью уже не позволяет трезво оценить ни наличную точность, ни наличную вечность полученных математических результатов, не говоря уже об их реальной, практической ценности.
Говоря кратко и в свете предстоящего повествования, современная (сиречь пост-канторовская) математика изучает конструкции, отношение которых к реальному миру по меньшей мере проблематично (см.: Вопенка П. Математика в альтернативной теории множеств). Так что, для начала, предоставим несчастным физикам (и не менее несчастным астрономам) выбиваться из сил, проверяя практический смысл канторовской (или уже, скорее, пост-канторовской) Теории множеств. Их неблагодарный и, скорее всего, вообще безнадёжный труд в этом направлении должен вызывать у математиков уж никак не презрение, но, по меньшей мере, сочувствие и сострадание.
Но даже и с вечностью достигнутых результатов отнюдь не всё гладко. Будет, конечно, уж совсем дурным тоном указать здесь на то, что недоказанность непротиворечивости Теории множеств непосредственно означает возможность обнаружения в ней противоречия, это всё так в силу одного факта недоказанности непротиворечивости. Тем не менее, даже над такой перспективой не должно, вообще говоря, смеяться.
Есть и масса совсем иных соображений, куда более тонких и отнюдь не менее устрашающих. Одно из них приводит П. Вопенка. Кратко говоря, суть в следующем.
Рассмотрение длинного ряда математических проблем (ужасы аксиомы выбора и многие другие ужасы) заставляет нас заново искать какие-то новые способы удостоверения в истинности и универсальности таких основополагающих принципов как принцип математической индукции. Просто-напросто потому, что картина складывается такая, что оказывается возможным (или не совсем невозможным) предположить убывание истинности доказательств с увеличением их длины (Вопенка, П. Математика в альтернативной теории множеств. С. 9-10). И это не говоря о многом и многом другом.
Так что Теория множеств всё время трещит по швам, и сейчас можно говорить о том, что это следствие наличия внутренних границ у науки, у математики, в частности; что существуют проблемы неразрешимые качественно, не только в связи с техническими сложностями, но в принципе выходящие за рамки человеческих способностей. Это удивительно тонко чувствовали древние, в этом воочию убедились и мы.
Так что упоение математикой, как и любое иное упоение, до добра довести не может. Деление людей на “геометров” и глупых людей – это деление глубоко затрудняющее плодотворную научную деятельность. И вообще, всегда необходима трезвая самооценка. Как мы увидим, этой математической самооценки весьма и весьма недоставало о. Флоренскому.
Математические воззрения отца Павла Флоренского
О. Флоренский и Кантор

Ещё студентом, о. Павел Флоренский начинает писать большую работу, посвящённую Г. Кантору и его идеям. Работа эта осталась неоконченной, написано лишь что-то вроде предисловия к так и не написанному: “Введение к диссертации “Идея прерывности как элемент миросозерцания” (опубликовано: Историко-математические исследования. Выпуск ХХХ. Москва: Наука, 1986. С. 159-176).
Отдельно была издана гораздо более известная статья «О символах бесконечности (Очерк идей Г. Кантора)» (см.: Сочинения в 4-х томах. Том 1. М.: Мысль, 1994. С. 79-128).
Сначала обратимся к предисловию к ненаписанному.
О. Флоренский здесь критикует лейбницевский подход к непрерывности и утверждает примат дискретности. Не непрерывность есть главный, скажем так, фактор и аспект бытия, но именно особенность и дискретность. Это очень хорошо, спору нет: из тюрьмы полной предопределённости и тотальной непрерывности вырываемся на свободу.
Сюрпризом оказывается аргументация – о. Флоренский предлагает, главным образом, чисто математические аргументы. Неожиданно оказывается, что спор о том, как устроен мир, будет носить внутриматематический характер. Внезапно мы попадаем из огня да в полымя. На математическую онтологию Лейбница реакция следует не менее математическая и, видимо, ещё «более» онтологическая, как будет видно из дальнейшего. Внезапно наша судьба снова оказывается в зависимости от тех или иных математических теорем.
Кто освободит нас от тяжкого ига лейбницевского интеграла, кто изведёт нас из царства мёртвых душ, точнее мёртвых монад? Оказывается, что нас спасёт нечто наподобие функции Дирихле. Только специфические и многоспасительные свойства функции Дирихле и в состоянии принести нам избавление. Ударим функцией Дирихле по интегралу Лейбница и, перейдя от непрерывности к дискретности, заживём весело и счастливо. Долой непрерывность. Да здравствует дискретность.
Но главный герой о. Флоренского, конечно же, Г. Кантор. Теория множеств даст ответы на все вопросы бытия. Итак, математика, говорит о. Флоренский, породила культ непрерывности, она его должна и разоблачить. Всё решит математика и главная вершина математической мысли – Теория множеств.
Центральным аргументом против всевластия непрерывности служит построенный Кантором ненепрерывный континуум, внутри которого можно провести тем не менее непрерывную линию. Сам Кантор так пишет по этому поводу, о. Флоренский цитирует:
Гипотеза непрерывности пространства есть, следовательно, не более как предположение, само по себе произвольное, о полном однозначном и взаимном соответствии между чисто арифметическим континуумом трёх измерений (x, y, z) и пространством, которое служит основанием мира явлений… Итак, мы приходим к замечательному выводу, что нельзя ничего заключать непосредственно из одного факта непрерывного движения к общей непрерывности пространства трёх измерений к такой непрерывности, какой мы её представляем себе, чтобы объяснить явление движения. Значит, можно предпринять опыт изменения механики, приложимый к пространствам той же породы, что и А (т.е. разрывный континуум с непрерывными линиями внутри).
Авторитетов принято хотя бы побаиваться, и если и начинать критиковать, то осторожно. Однако я, грешный, тут не побоюсь сказать, что данный пассаж Г. Кантора есть не что иное как наукообразный софизм, не содержащий вообще какой-либо содержательной мысли.
Если мы можем рассмотреть произвольный вымышленный объект, то это будет означать наличие у нас соответствующей возможности рассмотрения оного вымышленного объекта, говорит нам Кантор. В свою очередь вымышленность данного вымышленного объекта есть не что иное как важнейшее и неоспоримое свидетельство той произвольности, твёрдо руководствуясь которой, мы этот вымышленный объект измыслить с самого начала и соизволили. Убрать бы из этого суждения Кантора всего одно слово – “следовательно”, и всё обретало бы вполне реальный смысл: “Гипотеза непрерывности пространства есть не более как предположение” и т.д., без этого вот “следовательно”, и далее – рассмотрим другие модели для механики, и пусть опыт нас рассудит, и т.д. и т.п., всё ясно и в полном порядке.
Но совсем не этот здравый и научный смысл на уме у Кантора, неслучайно он ставит это “следовательно”. У него на уме совсем другие вещи, он, как и о. Флоренский, тоже живёт математической алхимией, а алхимик алхимика, конечно, видит издалека.
Будем, однако, точными: есть два пути придать смысл приведённому канторовскому пассажу. Либо вообще отказать ему в придании смысла, смыслом тогда явится смысл содержащийся в процессе переливания из пустого в порожнее. Это будет, впрочем, весьма обидно для крупного учёного. Либо второе – указать на алхимический образ мысли указанного крупного учёного. Это второе также принесёт немалый конфуз,
А между тем чуть ранее о. Флоренский процитировал Р. Дедекинда, который ровно об этом же пишет так: Если вообще пространство имеет реальное бытие, то ему нет надобности быть непрерывным. Бесчисленные его свойства оставались бы теми же, если бы оно было разрывным. И если бы мы не знали наверно, что пространство не обладает непрерывностью, то при желании нам всё-таки ничто не могло бы помешать сделать его непрерывным через мысленное заполнение пробелов его. Это заполнение должно было бы состоять в создании новых точек и осуществлялось бы сообразно упомянутому признаку.
Вот, собственно, и всё. Вот, чем следовало начать и этим же и закончить. Вот строго научный подход к сути дела. Наконец, к этому и свелась бы упомянутая выше цитата из Кантора без “следовательно”. Казалось бы, тут всё сказано, зачем далее огород городить? Но нет, это уж очень скучно, тут уж никакой романтики не обретается вовсе, а без романтики очень скучно, такая вот сухая наука далеко не всем по душе. Перспектива решения всех мировых проблем усилием воли (или мысли) – вот это куда как романтичнее.
Идём теперь далее, к статье о. Флоренского 1904 г., целиком посвящённой Г. Кантору. О. Флоренский с огромным энтузиазмом пытается защищать в этой статье идеи Кантора. Статья имеет ярко выраженный религиозно-мистический уклон, что на самом деле вполне соответствует первоисточнику – всё именно так и у самого Кантора. Долгое время статьи Кантора не принимались научными журналами с одним и тем же аргументом – очень много философии и очень мало математики.
Как пишет В.Н. Катасонов:
Говоря с математиками, Кантор был вынужден использовать философскую терминологию, чтобы хоть как-то оправдать всю необычность своих подходов, а полемизируя с философами, использовать свои новые математические конструкции, ибо только они могли конкретно показать ограниченность старых представлений… Кантор откровенно пишет: “Публикуя это сочинение, я не могу не упомянуть, что когда я писал его, то я имел в виду главным образом двоякого рода читателей: с одной стороны, философов, следивших за развитием математики вплоть до новейшего времени, а с другой — математиков, которые знакомы с важнейшими фактами древней и новой философии”. Как видим, требования к читателю были достаточно высокие. А поскольку большинство математиков и философов второй половины XIX века уже не удовлетворяло им, постольку работы Кантора раздражали как одних, так и других (Г. Кантор и проблема границ науки. С. 2).
Кроме того, сам о. Флоренский не занимается непосредственно математическими исследованиями, но, имея с математикой знакомство, ищет каких-то новых, прямо сказать, гностических синтезов, и финал статьи в этом отношении чересчур показателен.
Вероятно, все знают “пасхальную песнь” евреев. Вы помните, конечно, решительную настойчивость, грубо говоря, почти назойливость в мольбах к Богу. Эта неотступность в просьбе, это богоборство, “не отпущу, доколе не благословишь”, в высшей мере характерно для творчества Георга Кантора, и я думаю не смогу лучше окончательно разъяснить смысл его деятельности, как приводя текст этой песни. Вон он: “Боже Всемогущий, ныне близко и скоро храм Твой создай, скоро, в наши дни, как можно ближе, ныне создай, ныне создай, ныне создай, ныне близко храм Твой создай! Милосердный Боже, Великий Боже, кроткий Боже, всевышний Боже, благий Боже, сладчайший Боже, безмерный Боже, Боже Израилев, в близкое время храм Твой создай, скоро, скоро в дни наши, ныне создай, ныне создай, ныне создай, ныне создай, ныне скоро храм Твой создай! Могущественный Боже, живый Боже, крепкий Боже, славный Боже, милостивый Боже, царствующий Боже, богатый Боже, великолепный Боже, верный Боже, ныне не медля храм Твой восставь, скоро, скоро, в дни наши, не медля, скоро, ныне создай, ныне создай, ныне создай, ныне создай, ныне скоро храм Твой создай!”
Для человека православного очевидна вся религиозная двусмысленность такого пассажа, столь явный “экуменизм” вызывает некоторую, по меньшей мере, настороженность. Оставляя же это в стороне, отметим другое: а именно всю, так сказать, натуралистичность видения математики, столь характерную для о. Флоренского. Но и не просто натуралистичность – тут явно звучат мотивы мистические.
И всё же, как у нас с «храмостроительством», каковы на данный момент практические результаты? Подводя итог всему этому долгому и упорному “храмостроительству”, в конце 1970-х П. Вопенка напишет: Попытки математиков до конца постичь актуальную бесконечность оказались безуспешными. Но это не уменьшает, конечно, важности канторовской теории множеств, которая остаётся свидетельством стремления человека раздвинуть пределы пространства способом, не имеющим никакой аналогии в истории (Вопенка П. Математика в альтернативной теории множеств. С. 12). Таким образом, Вавилонскую башню возвести не удалось, но её развалины остались, они поражают и будут поражать самым непомерным величием своим, непомерным величием изначального замысла…
Статья о. Флоренского написана в 1904 г. и это обстоятельство является критическим для собственно математической стороны дела. На этот момент уже известны т.н. парадоксы Теории множеств, полным ходом идут поиски рецептов спасения канторовских построений, разваливающихся и расползающихся по швам, и мало этого, уже открылся и другой ящик математической Пандоры – начала свирепствовать аксиома выбора.
О. Флоренский всего этого удивительным образом не замечает, ведёт свой рассказ как ни в чём ни бывало. Более того, у читателя, не знакомого с положением дел в математике, скорее сложится представление, что математикой и философией тысячелетиями занимались лишь две категории людей – люди, близкие Г. Кантору и его идеям, и – с другой стороны – упрямые и завистливые невежды. Столь, мягко говоря, не соответствующий действительности вывод, который невольно должен сделать наивный читатель, будет всецело на совести о. Флоренского. И мы уже сейчас в связи с этим прямо обвиним о. Флоренского в научной недобросовестности.
Может, тем не менее, остаться некая тень неопределённости – в конце концов, прошло только два года, автор мог “не слышать” о появлении парадоксов, слухи из Европы до автора ещё не дошли и пр. Надо сказать, во-первых, что, даже если и так, то это само по себе довольно плохо, но во-вторых, пройдёт целых 18 лет, и в своей наиболее известной работе на математические темы (Мнимости в геометрии. М., 1922) о. Флоренский предпочтёт не то, что не обращать внимания на такие мелочи, он не только ни словом об этом не обмолвится, но и предложит разом зачеркнуть всю историю математики за целое столетие, чтобы, отправив в отставку Коши и Дирихле, вместе с Кантором отправляться в гости к Декарту.
Это не научно. В этом можно искать что угодно – эстетику, метафизику, “духовность”, что угодно, но только не науку.
Символов для ухватывания актуальной бесконечности не было,- пишет о. Флоренский,- и попытки создать их оказывались неудачны, пока упорный труд, неукротимая сила мышления и пламенная вера в успех не привели, наконец, Кантора к желаемой цели. Он показал, что такие символы можно создать, что не только абсолютный дух, но и мы можем иметь идею о бесконечном множестве.
Тут хочется привести другую цитату:
Со своей неслыханно смелой мыслью, что власть человеческой символики простирается и на Бога, Лейбниц вероятно сильнее всех философов ощутил тайный мотив, вдохновляющий этот штурмующий небо, разбивающий границы эйдетического мышления полет западной, нордически – германской в своем ядре математики (Becker, O. Mathematische Existenz. Halle, 1927. S. 288) (Катасонов, В.Н. Философско- религиозные проблемы науки нового времени. С. 90).
Хайль Лейбниц, но и, конечно же, хайль Кантор. А в самом деле, распространяется ли власть человеческой символики на Бога?..
Приводимый в самом начале статьи о. Флоренского 1904 г. пример множества понятий как множества актуально бесконечного уже два года как был исключён из рассмотрения парадоксом Рассела. Про множество понятий в сколь-нибудь математическом смысле говорить в 1904 году было уже безнадёжно поздно. Множество понятий самоприменимо – возможно понятие о понятиях, слово о словах, эдакий зеноновский парадокс места, и на совершенно законных притом основаниях. Но вот такие самоприменимые множества последовательно мыслить оказывается невозможно, возникают противоречия, например, иметь понятие об отсутствии всех понятий не представляется возможным.
Для науки противоречие – это катастрофа, конец науки. Нарушение закона тождества равносильно концу науки как таковой. Однако в высшей степени замечательно то, что о. Флоренский всю жизнь последовательно искал какого-то преодоления закона тождества, какое-то “всеединство” и “любезную ему непонятность”, так что противоречие для него не выглядит чем-то уж очень страшным. Скорее наоборот. В этом контексте полное игнорирование проблематики математических парадоксов у о. Флоренского будет очень и очень показательным.
Далее. Главные ошибки,- пишет автор,- которые делаются сплошь и рядом в рассуждениях о бесконечном, появляются вследствие пренебрежения основной и совершенно элементарной дистинкцией актуальной и потенциальной бесконечности. Т.е. оппоненты Кантора суть люди невежественные, они не понимают, что говорят. Т.е. когда кто-то говорит, что единица есть начало множества, этот кто-то не понимает всей своей умственной ограниченности, он не понимает, что говорит лишь о бесконечности потенциальной, ему-то между тем говорят об актуальной бесконечности.
В действительности всё совсем иначе. Оппоненты Кантора всё хорошо понимали. Понимали, и именно потому и возражали. Смысл возражений как раз и состоял в требовании отделить то, что нам “дано”, от того, что нам “не дано”. Единица потому и есть начало множества, что интуиция счёта есть интуиция глубочайшая, связанная с самыми основаниями мышления, самой способности рассуждать. Теорема Левенгейма-Сколема позже это обстоятельство подчеркнёт. Выяснится, что никакие “несчётные” множества человеческое сознание эффективно мыслить не в состоянии. И речь была как раз о том, чтó мы мыслить в состоянии, а чтó нет.
На единственности интуиции потенциальной бесконечности потому и настаивали, что считали только её “данной” человеческому сознанию. Бесконечность актуальную считали никак не данной, её не считали всего лишь просто “другой”, но, напротив, считали вообще немыслимой.
Кантор настаивал на том, что актуальная бесконечность “дана” наравне с потенциальной, и надо просто их различать. Смысл же противоположных аргументов был в ином – в том, что отнюдь никак не дана нам актуальная бесконечность, следовательно, все попытки с ней оперировать будут самообманом. О. Флоренский наблюдает за этой полемикой со стороны. Со стороны вроде бы должно быть виднее, но несмотря на это он ничего кроме повторения канторовских аргументов вниманию читателя не предлагает.
Как же “дана” нам актуальная бесконечность? Это и есть тонкое место, заслуживающее самого пристального внимания, а отнюдь не упоминания вскользь, как у о. Флоренского в разбираемой нами статье. Сам Кантор это хорошо чувствовал, и у него тут имелось только одно средство – чисто логическое. Т.е. явочным порядком ввести в рассмотрение бесконечные числа наравне с конечными. И он определяет некоторые правила, по которым можно что-то действительно делать с этими вновь введёнными числами. Но при этом возникают совершенно новые вопросы. Прежде всего, насколько надёжны сами эти правила?
Кантор говорит, что он “доказал” существование трансфинитного посредством простого введения правил оперирования с ним. Какая, однако, самонадеянная наивность! Надо бы, в самом деле, как-нибудь обосновать эти новые правила!
Но этот же аргумент повторяет и о. Флоренский – уже после того, как обнаружены парадоксы, когда эти вот вновь введённые правила оказались под конкретным, и очень большим, вопросом, и потому сама возможность доказать законность новых операций (а вместе и существование самого трансфинитного “как такового”!) оказалась весьма проблематичной. Так относиться к делу нельзя. Это не научно. Видеть только то, что хочется видеть, это просто и не серьёзно в конце концов.
Возьмем примеры более конкретные. Например, обращаясь к пространству, мы можем утверждать, что все точки внутри некоторой замкнутой поверхности образуют множество актуально-бесконечное,- пишет о. Флоренский. В таком вот “конкретном примере” как в капле воды отражается вся, попросту говоря, ошибочность проканторовской аргументации. Данная ошибка с древности называется petitio principii, или предвосхищение основания.
Дело в том, что сама возможность таким именно образом “обратиться” к пространству должна была бы стать конечным результатом, главным триумфом Теории множеств! Не посылкой, а конечным результатом!
Если каким-то образом убрать парадоксы, и затем доказать континуум-гипотезу, а попутно для верности ещё и доказать формальную непротиворечивость по Гильберту, вот тогда мы приходим к арифметизации континуума, тогда – и только тогда! – мы получаем вполне законное право воспринимать отрезок как совокупность непротяжённых точек. Тогда падают аргументы Зенона и преодолевается пропасть между дискретным и непрерывным!
Но прав был Зенон, и всё перечисленное возможно лишь только в сладких снах.
В 1904 году уже явились парадоксы, континуум-гипотезу доказать никак не удаётся и не удастся уже никогда (в психиатрической лечебнице Кантор оказывается именно из-за переутомлений, связанных с безуспешными попытками её доказать). Непротиворечивость доказать также будет невозможно, на момент написания статьи ещё не начинались и попытки это сделать, но несмотря ни на что о. Флоренский предпочитает мир сладких снов. Впрочем, для него эти сны и составляют подлинную реальность…
Суть дела прекрасно обрисовывает Катасонов.
Аристотель говорит, что бесконечное уничтожает конечное. По канторовским правилам это не всегда так. Чисто математические детали легко посмотреть в многочисленной литературе, как и в разбираемой статье о. Флоренского. Итак:
Только обратное действие, именно прибавление бесконечного числа к конечному, когда сначала полагается конечное число, вызывает уничтожение последнего, не приводя к модификации первого. Эта правильная точка зрения на отношение между конечным и бесконечным, совершенно неизвестная Аристотелю, должна была бы вызвать новые идеи не только в анализе, но и в других науках, особенно в естествознании”. Невольно хочется здесь защитить Аристотеля. То, что эта точка зрения правильная — это еще под вопросом. То, что представлено, есть лишь некоторая точка зрения. Некоторая интерпретация аристотелевских рассуждений. И, главное, Аристотель скорее бы не согласился с такой интерпретацией. То есть это не было бы ответом на его рассуждения. Потому, что эта интерпретация связана с принятием многих предпосылок, которые чужды и Аристотелю, и античной мысли вообще.
Здесь налицо та самая несоизмеримость научных теорий, о которой столь пространно писал Т. Кун. Вводятся новые понятия и строятся новые научные теории, которые претендуют решить старые неразрешенные задачи. Однако эти новые решения существенно связаны с введением новых объектов, научный статус которых (онтологический ли, или просто логический) сам достаточно проблематичен. Для науки нового времени актуальная бесконечность постоянно играла роль подобного объекта. Так Лейбниц “решил” задачу квадратуры круга: он “вычислил” площадь круга, т.е. выразил ее с помощью бесконечного ряда. Однако что это за объект – бесконечный ряд, легально ли его введение в математику, каковы необходимые логические предпосылки этого введения – все эти вопросы оставались по существу открытыми вплоть до XIX века. По существу произошла замена одной проблемы на другую. Можно ли это считать решением задачи квадратуры круга, как ее понимала античность? Канторовское настойчивое желание ввести “бесконечные числа” грешит все тем же: игнорированием логических границ между старой и новой теорией. Нужно было почти столетнее усилие методологической философской мысли, чтобы сегодня на пороге нового века мы научились лучше различать границы различных эпистем (Катасонов В.Н. Г. Кантор и проблема границ науки. С. 7).
Вот какова научная сторона вопроса.
О. Флоренскому всё это в принципе не интересно. Ему не интересна наука. Его интересует некое гностическое околоматематическое фэнтези. Или, лучше скажем, алхимия.
“Не геометр да не войдёт” – знаменитая надпись на дверях платоновской академии. Восприятие математики как средства для познания “чистых идей” суть древнейшее. Но и более общим образом: желание видеть математику независимой от всякого эмпирического опыта, можно сказать, красной нитью проходит через историю науки.
Возникает другой вопрос – что же такое эмпиризм? Созерцание идей это “эмпиризм” или нет? Математические “идеи” составляют ли реальность, которая “эмпирически” созерцается на ином, более высоком уровне “эмпиризма”, или слово “созерцание” тут лишь метафора и не более того?
Видеть математику независимой от опыта, от эксперимента в широком смысле, видеть её наукой о “вечных” истинах хотели очень многие, и вообще едва ли не большинство математиков. Вот что пишет Вопенка: Математика есть способ преодоления непосредственного горизонта человеческого опыта. Мы используем математику, чтобы выразить мысли, предваряющие наше знание, которое часто в дальнейшем нельзя проверить (Вопенка П. Математика в альтернативной теории множеств. С. 15). К этой цитате мы ещё вернёмся.
“Априорности” в математике всегда искал Б. Рассел. Его в советской литературе постоянно, хотя и сдержанно – всё-таки как никак атеист, борец за мир и пр. – обвиняли в платонизме и вообще в “метафизике”. И в самом деле, его Теорию типов надо признать весьма и весьма “платонической”. Теория типов воспринимает математику как “данность”, как законченное целое, и аксиома сводимости представляет собой квинтэссенцию этого вот “платонического” подхода к математике. Но как вообще появилась Теория типов? Как способ обоснования Теории множеств, как реакция на возникшие трудности в виде парадоксов. Таким образом, платонизм Рассела это дело, так сказать, локальное, внутринаучное. Рассматриваются наличные научные проблемы под определённым углом зрения с большим или меньшим успехом.
Но совсем не таков платонизм о. Флоренского: тут научные проблемы, как именно научные, вообще не рассматриваются, цели и задачи тут совсем другие.
В моем мировоззрении физического как такового, т.е. вне его пронизанности духовными и оккультными энергиями, вовсе не существует, и я полагаю, что не магическое надо объяснять физическими причинами, но напротив, так называемое или кажущееся профанам физическим подлежит объяснению через магические силы (Флоренский П., о. У водоразделов мысли // Сочинения в 4-х т. М.: Мысль, 2001. Т. 3(1). С. 233). Тут и магия, и оккультное, наконец, самое словечко “профан” – всё это из совсем иных сфер. Автор говорит о “магии слова”, о том, как словом мы “воздействуем на мир”, о слове, как о “явлении смысла”. Всё это платонизм совершенно иного уровня, платонизм уже “онтологический”, вполне магический и алхимический.
Если слово есть явление смысла, то, очевидно, математика эти “смыслы” имеет своим предметом, притом во вполне “эмпирическом” отношении. Математическое здесь оказывается процессом непосредственных и вполне “эмпирических” созерцаний, да ещё и таких, для которых закон тождества будет чем-то второстепенным. Видеть математику независимой от закона тождества не отваживался даже Платон. О. Флоренский отваживается.
О своём отношении к закону тождества в своих двух математических работах о. Флоренский не говорит. Но, во-первых, он ничего не говорит и о парадоксах Теории множеств, и во-вторых, о законе тождества достаточно сказано в других его работах.
В “Столпе” автор говорит о Боге как об онтологическом бытийном противоречии. Противоречие у автора предстаёт укоренённым в Боге. Значит, пока разум держится за закон тождества, истину он разуметь не может. Только лишь возвысившись над тождеством, перейдя к противоречию, разум и может обрести истину. Всё это не только странно, это и выразить-то связно не получается – просто в силу того факта, что связность сама по себе опирается на тождество. Сам о. Флоренский, как ни пытается, не может определиться с используемыми им понятиями разума, рассудка, веры и пр. (см. Гайденко П. П. Антиномическая диалектика П.А. Флоренского против закона тождества).
Это вполне естественно. Однажды отвергнув закон тождества, уже никогда не сможешь связно рассуждать. Скажем здесь ещё лишь о том, что у самого мистического и “антиномического” из Св. Отцов, у Дионисия Ареопагита, о Боге говорится, что Он есть Единство превыше единства, и Троица превосходит Единство – не в том смысле, что начинается реальность противоречивая, но наоборот: Троица ещё более едина, чем Единица. Свт. Дионисий Ареопагит, таким образом, говорит не о противоречии в Боге, но о Сверхъединстве, Единстве превыше единства, о Единстве вообще непомыслимом, дверью к которому будет не какое-то бытийное противоречие и распад, но, напротив, состояние “целомудрия”, когда Божественная благодать собирает все силы души в несказанное единство и самотождество. Со св. Дионисием Ареопагитом о. Флоренскому явно не по пути. Зато по пути с Кантором.
В. Н. Катасонов отмечает, что для Кантора Теория множеств была чистой метафизикой, средством мыслить Божественное, иерархия трансфинитных чисел была для него как “лестница на небо”. Сумма же всех порядковых чисел виделась имеющей некий совершенно уже мистический смысл. И отнюдь не случайно, что Кантор не стал первым говорить о том, что эта сумма будет больше самой себя (парадокс Бурали-Форти; Кантор это видел, но не захотел портить праздник, спустя пару лет Бурали-Форти выразил свои опасения по этому поводу, и парадокс с тех пор носит его имя).
Может быть, Кантору тут даже виделись упомянутые мотивы из св. Дионисия Ареопагита, но в любом случае для Кантора этот факт был чем-то “нормальным”, “бытийственным”: всё так и должно было бы быть, тут выход, дверь в вечность, рассудок умолкает. Но что с этим делать, что будет значить это молчание рассудка для дела развития математики, Кантор так и не решил. Апеллировать к своим мистическим переживаниям на страницах математических журналов он не отважился, и подробности нам не известны.
О. Флоренский видит в Канторе родственную душу. По крайней мере, он молчит о парадоксах совершенно по-канторовски.
Мнимости в математике
В этом свете становится понятной первоначальная установка на “созерцательность” в “Мнимостях в геометрии”. Рациональное определение понятия функции в смысле Коши и Дирихле решительно отвергается. Рассматривать предлагается не иначе как “саму функцию”, функцию как чистую форму, как целое – остаётся только сказать что-нибудь о “чистом духе”, “идеях”, и заодно о Гермесе Трисмегисте.

О “математической реальности” можно что-нибудь найти во многих книгах по математике, но всегда в смысле более или менее метафорическом. О. Флоренский, однако, говорит совсем о другом.
Научные картины одной и той же реальности должны быть умножаемы. Чуть выше читаем, что плоскость комплексного переменного не есть самое переменное, это только интерпретация, символически являющая, но не исчерпывающая соответственных математических сущностей.
Кажется, мне нигде не приходилось слышать ни о “математических сущностях”, ни о различении “самого” комплексного переменного от соотв. плоскости. Наоборот, одно было тождественным другому, в этом и весь смысл аналитической геометрии – в тождественности функции и её графика, точнее, с учётом вышесказанного, в стремлении к такой тождественности.
Построение математической интерпретации даже в смысле интерпретации физической недопустимо, а у о. Флоренского слышатся мотивы чуть ли не поэтические. Наличествуют, бытийствуют “математические сущности”, и математик, подобно искусному живописцу, живописует их в своих “интерпретациях” то в профиль, то в анфас. То так, то эдак призван математик рассматривать недоступные рациональному познанию “сущности”, в изобилии населяющие математические глубины.
Цитата из Герца окончательно проясняет положение: Всякое истолкование подлежит тому, что сказано Г. Герцем о картинах мира: это есть система образов, взятых произвольно, но соответствующих системе истолковываемой, и притом так, чтобы возможно большее число следствий из принятых истолковывающих образов соответствовало последствиям системы истолковываемой (Мнимости в геометрии. М. Лазурь, 1991. С. 8).
Герц ведь говорит здесь об интерпретациях в смысле науки физической, о картинах мира. Значит, о. Флоренский видит математику тоже как “мир”, где есть “сущность” и “явление”, “воля” и “представление”, и где загадочная и величественная “сущность” комплексного числа лишь слабо отражается в тусклом зеркале комплексной плоскости.
Вопрос о существовании математических объектов чрезвычайно сложен, решение этого вопроса во многом зависит от тех или иных убеждений, и более того, верований людей, занимающихся математикой, и, разумеется, от возможности компромисса между этими людьми.
Как и в каком смысле “существует” мнимая единица? Что это такое? Можно ли счесть, что она была “открыта” наподобие того, как был открыт Уран или Нептун?
Один из крупнейших математиков XIX века Л. Кронекер говорил, что Бог создал натуральные числа, а остальное дело рук человеческих. Очень важно то, что за этими словами стоит его личный опыт философских разочарований. Поиски философской истины ни к чему Кронекера не привели, и взгляд его на математику поэтому стал в высшей степени “аскетическим”.
Глубоко прислушавшись к самим себе, мы находим интуицию счёта лежащей в самом основании нашего мышления и мировосприятия. С другой стороны, Писание говорит: Вся мерою и числом расположил еси (Прем. Сол. 11:21).
Утверждение о том, что единица есть начало множества, открывается как исключительное и поистине “единственное”. Наука должна быть как можно более независимой от личных убеждений, и в чём же тогда будут её основания? В том, что наиболее безусловно. Только там, писал Кронекер Кантору, где математику удалось свести к целым числам, только там и можно видеть действительный прогресс.
Не удалось всё вообще свести к целым числам – ну что же, да, верно, не удалось. Но где будет математический “идеал”, к чему надо стремиться? К целым числам. Только там прогресс, только там ясность.
Посмотрим с этой точки зрения на мнимую единицу. Этот совершенно “невозможный” и поистине “мнимый” математический объект вводится так, чтобы его введение ничему не помешало, чтобы его можно было бы при желании вообще не замечать, используя переменные без уточнения, действительные они или комплексные. Но производимые при этом “мнимые” вычисления оказываются имеющими реальный и вполне “действительный” результат, практическая польза вычислений оказывается огромной. Практика оказывается критерием истины. Упрощение одних вычислений и появление совсем новых вычислительных методов – это и есть оправдание “существования” мнимой единицы. Так и по Кронекеру, так и по самому естественному здравому смыслу.
Альтернативу видим у о. Флоренского: самый радикальный платонизм, а по существу – алхимия. Мнимая единица существует, существует сама по себе, её надо изучать как таковую. Различные геометрические интерпретации будут являть нам её сущность с разных сторон, да так никогда оную сущность до конца и не явят, ибо тайна сей сущности велика есть.
Вообще говоря, именно в этом месте возразить по большому счёту и нечего. Верит человек в математические реалии, верит и всё. И всё же некоторые возражения оказывается возможным привести, точнее, такую возможность чуть позже нам предоставит сам о. Флоренский, когда его вычисления границы миров окажутся ошибочными.
О реках, текущих внутри прозрачной, совсем без толщины, плоскости, обо всём таком говорить сложно. Сам о. Флоренский пишет: Итак, согласно предлагаемому толкованию мнимостей, кривая может уходить с лица поверхности вглубь ее толщи и тогда протекает на том или другом участке своего течения наподобие подземных рек, изображаемых на карте пунктиром, – чтобы затем найти себе выход наружу.
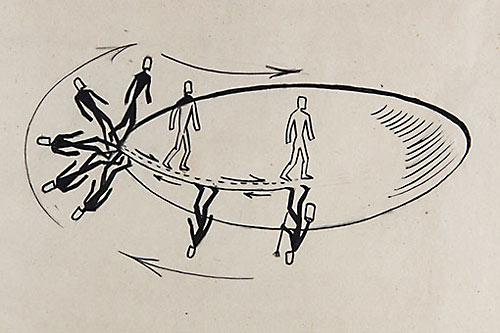
Автор там же оговаривается, что понятие актуально бесконечно-малого в науке точно не разработано, употреблять такое понятие поэтому затруднительно и пр., но реки у о. Флоренского при этом продолжают течь. И течь внутри плоскости без толщины. Т.е. понятия-то вроде бы нет, но оно вроде как есть. Ничего что его нет, это не беда, все равно оно будет, всё равно всё будет хорошо.
Декарт писал, что привычка и пример убеждают более, нежели рациональные соображения. А Геббельс вообще требовал повторять “одно и то же”, невзирая на “возражения интеллектуалов”. Во всей аргументации в пользу Теории множеств с самого начала, начиная от самого Кантора, постоянно видится сильное желание “заговорить” вопрос, повторениями “одного и того же” – всё нам уже дано, дано, дано, надо лишь изучать, изучать, изучать – создать эффект привыкания, заставить читателя привыкнуть и через это умолкнуть, перестать возражать. В наши дни всё это в миниатюре переживают студенты математических ВУЗов на семинарах под многозначительные улыбки преподавателей.
Так и здесь.
Плоскость бесконечно тонка, понятия об этом нет, но тем не менее она “видится” бесконечно тонкой со всей истинно декартовской “ясностью и отчётливостью”. А если вам не понятно, тогда что с вами говорить…
Мнимости во Вселенной
В заключительной части “Мнимостей в геометрии” предложенная автором геометрическая (лучше же сказать, окологеометрическая) интерпретация мнимостей будет использована для нужд астрономии.
Отправной точкой рассуждений берётся вселенная Данте. Путешествие его (Данте) было действительностью; но если бы кто стал отрицать последнее, то во всяком случае оно должно быть признано поэтическою действительностью, т.е. представимым и мыслимым, значит, содержащим в себе данные для уяснения его геометрических предпосылок (Мнимости в геометрии. М. Лазурь, 1991. С. 46).
Т.е. то, что написал Данте, так или иначе рассматривается в качестве факта научного и физического, как если бы Данте был великим путешественником, специализацией которого были путешествия по кругам ада. Всё написанное Данте воспринимается как реальный научный факт, точнее же сказать, достоверный факт научной мистики, и таким образом “научный мистицизм” – вот предмет наших занятий. В самом худшем случае, как явствует из пояснительной оговорки автора, речь идёт о “действительности поэтической”.
Что такое “поэтическая действительность”? Чем она отличается от действительности “непоэтической”? Всё это, однако, понять вряд ли возможно. Писания о. Флоренского вообще изобилуют разнообразными терминами, смысл которых более чем неясен.
Честно говоря, я такие вот термины, как этот, у о. Флоренского воспринимаю как некие софистические уловки, мол, я сейчас скажу нечто странное и нелепое, но сразу оговорюсь, я ничего странного и нелепого говорить не буду, всё будет строго по науке, ничего ненаучного тут не будет, итак, перейду к моей высоконаучной нелепости.
Нежелание говорить прямо, уход от ответственности, заодно и окончательное запутывание читателя и окончательное формирование атмосферы “любезной (о. Флоренскому) непонятности”, т.е. атмосферы, в которой вообще никто вообще ничего понимать уже не будет: вот как лично я интерпретирую введение термина “поэтическая действительность”.
Осмелюсь поэтому вообще проигнорировать данное авторское “пояснение”, запутывающее дело, и говорить в дальнейшем просто о действительности и о реальности, как их понимает о. Флоренский. Т.е. реальность тут суть реальность в платоновском мистическом смысле слова. Насколько же будет “реальна” сама такая вот “реальность” – это уже совсем другой вопрос.
Поэтому будем просто считать, что имеем дело с “научным мистицизмом”. Математика, как известно, суть “царица наук”, так что и такой вот “научный мистицизм” без неё не обойдётся никак, математика будет здесь служить средством анализа мистических переживаний.
Мистическая, так сказать, ультраплатоническая и алхимическая математика и, с другой стороны, реалистичная, совершенно фактическая до полной “научности” мистика – вот каков мир о. Флоренского. И одно будет неотделимо от другого, как физика неотделима от физического мира, от камней, сил тяготения и электричества, так математика оказывается неотделимой от путешествий по кругам ада. Пытаясь схватить за хвост мнимую единицу, мы в итоге окажемся примерно там, где побывал Данте. Горькая ирония здесь в том, что это в сущности своей глубоко верно, только вот в совершенно другом смысле…
Итак, по о. Флоренскому, изучающий математику непосредственно и напрямую познаёт некий мир идей в платоновском и даже ультраплатоновском смысле слова, и такое познание обещает очень и очень многое. В том числе уяснение структуры ада с возможностью в нём ориентироваться. А также выяснение местоположения границы между миром и антимиром.
Сам по себе вопрос о вращении, о том, что, вокруг чего и как вращается, отнюдь не столь прост как может показаться. Большинство школьных учебников дают несколько искажённую картину сути дела. Во-первых, Джордано Бруно не был астрономом. Коперника он называл ничтожеством и невеждой, и массивные протоколы его допросов в инквизиции не содержат вообще ни слова на какие-либо астрономические темы. Это не оправдывает, мягко говоря, методы инквизиции, но предельно важно то, что к науке дело Джордано Бруно не имело вообще никакого отношения.
Далее, Галилей отрёкся не совсем от того, от чего принято думать, именно он отрёкся от своих утверждений о том, что Солнце является “центром мира”. Данный термин заимствован из Гермеса Трисмегиста, это по сути дела не иначе как солнцепоклонство. Аберрация открыта не была, Теории относительности не было и в помине, так что отречься от солнцепоклонства было совсем не зазорно.
Позже была открыта аберрация, затем появилась Теория относительности, и стало в общем и целом ясно, что Земля всё-же вращается. Но вот в каком смысле и как? На экваторе тяготение меньше чем на полюсах – откуда предметы, перемещаясь к экватору, узнают, что должны терять в весе? Возьмём ведро с водой. Если всё в мире относительно, как нам говорит соотв. теория, тогда не должно быть разницы, покрутим ли мы ведро или воду внутри ведра, и ведро, и вода суть глупые, они ни о чём не должны догадаться. Но нет, если крутить будем воду, тогда и только тогда середина просядет, если же крутить будем ведро, вода будет “покоиться”. Вращение, вопреки Теории относительности, оказывается отнюдь никак не относительным, но как раз весьма и весьма абсолютным. Вопрос о том, как это объяснить, далёк от какого-либо разрешения.
Где искать эту абсолютную опору, каркас и носитель стабильности пространства? И вот тут и появляется мысль о “всемирном эфире”. Попытка обнаружить “эфир” в самом что ни на есть старинном смысле слова есть попытка глубоко научная, попытка насущная, насущная для первейших нужд современной науки, ничего общего не имеющая с поисками философских камней и производством золота. И тот факт, что попытки эти ни к чему – пока! – не привели, только осложняет дело.
Так что, как говорится, проблема существует. Но подходит к ней о. Флоренский самым радикально ультракавалерийским способом. Эффект аберрации отбрасывается как несущественный. Мировой эфир считается фактически данным – это следующая предпосылка, а поэтому неудача с его обнаружением означает только то, что Земля покоится. Далее измеряем радиус небесной сферы и имеем границу мира между Ураном и Нептуном, за этой границей мир переворачивается, бегают мнимые единицы и вообще творится что-то невообразимое. И всё это мы узнаём благодаря силе математики. Математик благодаря математике проходит через пространство и время. Математик благодаря математике может всё.
Но отнюдь не всем по душе такое вот “всемогущество”. Не всем по душе услышать математическое доказательство переворота вселенной в районе орбиты Урана. Напротив, услышав о таком “доказательстве”, большинство математиков сразу заподозрит неладное, притом неладное именно в самом доказательстве.
Снова обратимся к словам П. Вопенки: Математика есть способ преодоления непосредственного горизонта человеческого опыта. Мы используем математику, чтобы выразить мысли, предваряющие наше знание, которое часто в дальнейшем нельзя проверить.
Плохой способ преодоления горизонта опыта выбрал о. Флоренский. Этот самый непосредственный горизонт нашего опыта за прошедшие десятилетия значительно расширился. К отдалённым планетам полетели космические аппараты и ни наизнанку при этом не вывернулись, ни с мнимыми единицами не столкнулись. Мы видим, что о. Флоренский ошибался в своих математических расчётах. Именно таких ошибок и опасается математика. Именно поэтому математика ищет наиболее надёжные основания, именно поэтому держится за идеи Коши и Дирихле, боится парадоксов и не спешит рассматривать течение рек внутри прозрачной плоскости. Преодоление горизонта опыта есть дело весьма и весьма ответственное, в этом деле очень опасно предаваться каким бы то ни было фантазиям.
Заключение
Итак, мы видели, что помимо двух главных путей в математике, условно их можно назвать формализмом и эмпиризмом по отношению к вопросу о зависимости или независимости математики от непосредственного опыта, есть ещё и некий третий путь – алхимизм. Подобно реке внутри математических плоскостей скрывается сей алхимизм от посторонних глаз, лишь изредка показываясь на поверхность. В писаниях о. Флоренского этот алхимизм показал себя вполне.
О. Флоренский в своих математических опусах, во-первых, игнорировал вопросы математической строгости, не чувствуя, по-видимому, вообще что это такое, и зачем она нужна, эта математическая строгость, и во-вторых, воспринимал математику до крайности реалистично, алхимически натуралистично, до того, что поэма Данте для него была непосредственным объектом математического исследования и одновременно источником математических сведений. Мы видим, что на этом пути о. Флоренский пришёл к ошибочным результатам. И вряд ли могло быть иначе.
Математика это не игра, и не алхимия. Математика требует строгости.
Христианская вера – тоже.
Но это уже тема богословия, а не математики.
Владислав Ломанов
Библиография
Френкель А.; Бар-Хиллел И. Основания теории множеств. М.: Мир, 1966
Вопенка П. Математика в альтернативной теории множеств. М.: Мир, 1983
Рассел Б. История западной философии. В 3 кн. Новосибирск: Сиб. унив. изд-во; Изд-во Новосиб. ун-та, 2001
Катасонов В. Н. Боровшийся с бесконечным. Философско-религиозные аспекты генезиса теории множеств Г. Кантора. М.: Мартис, 1999
Катасонов В. Н. Метафизическая математика XVII века. М.: Наука, 1993
Катасонов В.Н. Лестница на небо: генезис теории множеств Г. Кантора и проблема границ науки // Границы науки. М.: ИФ РАН, 2000
Гайденко П.П. Антиномическая диалектика П.А. Флоренского против закона тождества // Критика немарксистских концепций диалектики XX века. Диалектика и проблема иррационального. М.: Изд-во МГУ, 1988
Йейтс, Франсес. Джордано Бруно и герметическая традиция. М.: Новое литературное обозрение, 2000


